Python: Check whether a given sequence is linear, quadratic or cubic

Last update on December 21 2024 07:18:47 (UTC/GMT +8 hours)

Sequence Type Identifier

Write a Python program to check whether a given sequence is linear, quadratic or cubic.

Sequences are sets of numbers that are connected in some way.
Linear sequence:
A number pattern which increases or decreases by the same amount each time is called a linear sequence. The amount it increases or decreases by is known as the common difference.
Quadratic sequence:
In quadratic sequence, the difference between each term increases, or decreases, at a constant rate.
Cubic sequence:
Sequences where the 3rd difference are known as cubic sequence.

Sample Solution:

Python Code:

# Define a function named Seq_Linear_Quadratic_Cubic that takes a sequence of numbers (seq_nums) as an argument.
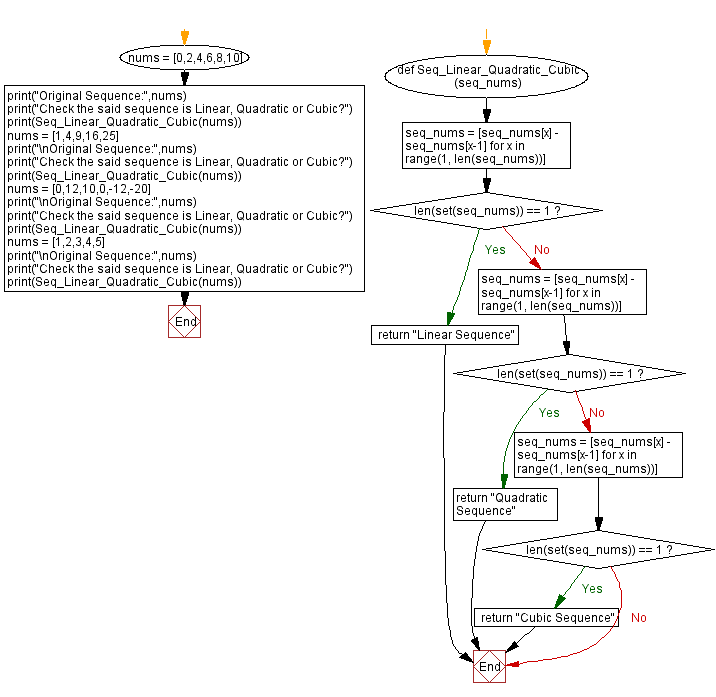
def Seq_Linear_Quadratic_Cubic(seq_nums):
    # Calculate the first-order differences between consecutive elements in the sequence.
    seq_nums = [seq_nums[x] - seq_nums[x-1] for x in range(1, len(seq_nums))]
    
    # Check if all differences are the same, indicating a linear sequence.
    if len(set(seq_nums)) == 1:
        return "Linear Sequence"
    
    # Calculate the second-order differences between consecutive elements in the modified sequence.
    seq_nums = [seq_nums[x] - seq_nums[x-1] for x in range(1, len(seq_nums))]
    
    # Check if all differences are the same, indicating a quadratic sequence.
    if len(set(seq_nums)) == 1:
        return "Quadratic Sequence"
    
    # Calculate the third-order differences between consecutive elements in the modified sequence.
    seq_nums = [seq_nums[x] - seq_nums[x-1] for x in range(1, len(seq_nums))]
    
    # Check if all differences are the same, indicating a cubic sequence.
    if len(set(seq_nums)) == 1:
        return "Cubic Sequence"

# Test the function with different sequences and print the results.

# Test case 1
nums = [0,2,4,6,8,10]
print("Original Sequence:", nums)
print("Check the said sequence is Linear, Quadratic, or Cubic?")
print(Seq_Linear_Quadratic_Cubic(nums))

# Test case 2
nums = [1,4,9,16,25]
print("\nOriginal Sequence:", nums)
print("Check the said sequence is Linear, Quadratic, or Cubic?")
print(Seq_Linear_Quadratic_Cubic(nums))

# Test case 3
nums = [0,12,10,0,-12,-20]
print("\nOriginal Sequence:", nums)
print("Check the said sequence is Linear, Quadratic, or Cubic?")
print(Seq_Linear_Quadratic_Cubic(nums))

# Test case 4
nums = [1,2,3,4,5]
print("\nOriginal Sequence:", nums)
print("Check the said sequence is Linear, Quadratic, or Cubic?")
print(Seq_Linear_Quadratic_Cubic(nums))

Sample Output:

Original Sequence: [0, 2, 4, 6, 8, 10]
Check the said sequence is Linear, Quadratic or Cubic?
Linear Sequence

Original Sequence: [1, 4, 9, 16, 25]
Check the said sequence is Linear, Quadratic or Cubic?
Quadratic Sequence

Original Sequence: [0, 12, 10, 0, -12, -20]
Check the said sequence is Linear, Quadratic or Cubic?
Cubic Sequence

Original Sequence: [1, 2, 3, 4, 5]
Check the said sequence is Linear, Quadratic or Cubic?
Linear Sequence

Explanation:

Here is a breakdown of the above Python code:

Function definition:

The code defines a function named "Seq_Linear_Quadratic_Cubic()" that takes a sequence of numbers (seq_nums) as an argument.

First-Order Differences:

The function calculates the first-order differences between consecutive elements in the sequence.

Linear Sequence Check:

The function checks if all differences are the same, indicating a linear sequence.

Second-Order Differences:

If the sequence is not linear, the function calculates the second-order differences between consecutive elements in the modified sequence.

Quadratic Sequence Check:

The function checks if all differences are the same, indicating a quadratic sequence.

Third-Order Differences:

If the sequence is not quadratic, the function calculates the third-order differences between consecutive elements in the modified sequence.

Cubic Sequence Check:

The function checks if all differences are the same, indicating a cubic sequence.

Flowchart:

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

Previous: Write a Python program to find a number in a given matrix, which is maximum in its column and minimum in its row.
Next: Write a Python program to test whether a given integer is Pandigital number or not.