Python: Find the type of the progression and the next successive member of a given three successive members of a sequence

Last update on December 21 2024 07:19:18 (UTC/GMT +8 hours)

Progression Type and Next

Write a Python program to find the type of the progression (arithmetic progression / geometric progression) and the next successive member of the three successive members of a sequence.

According to Wikipedia, an arithmetic progression (AP) is a sequence of numbers such that the difference of any two successive members of the sequence is a constant. For instance, the sequence 3, 5, 7, 9, 11, 13, . . . is an arithmetic progression with common difference 2. For this problem, we will limit ourselves to arithmetic progression whose common difference is a non-zero integer. On the other hand, a geometric progression (GP) is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, . . . is a geometric progression with common ratio 3. For this problem, we will limit ourselves to geometric progression whose common ratio is a non-zero integer.

Sample Solution:

Python Code:

# Define a function 'ap_gp_sequence' that identifies whether a given sequence is an Arithmetic Progression (AP) or Geometric Progression (GP).
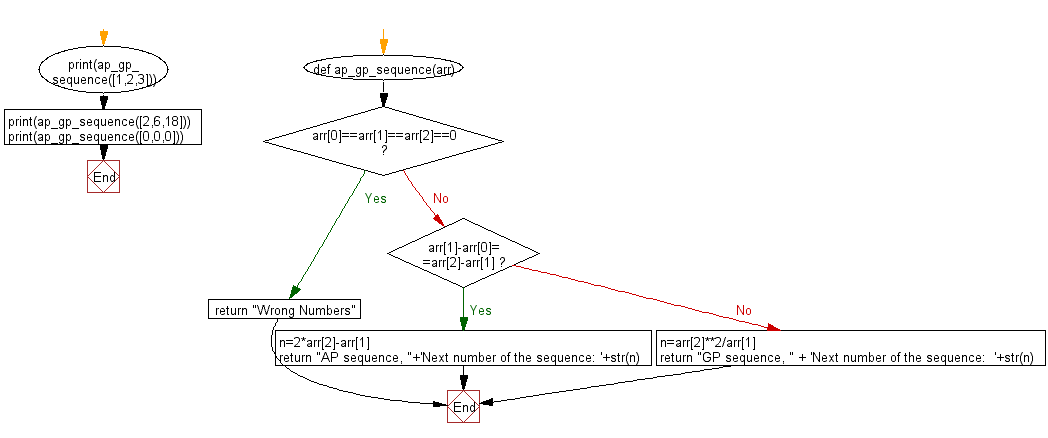
def ap_gp_sequence(arr):
    # Check if the first three elements are all zero.
    if arr[0] == arr[1] == arr[2] == 0:
        return "Wrong Numbers"  # If all three are zero, it's not a valid sequence.
    else:
        # Check if the sequence is an AP (Arithmetic Progression).
        if arr[1] - arr[0] == arr[2] - arr[1]:
            n = 2 * arr[2] - arr[1]
            return "AP sequence, " + 'Next number of the sequence: ' + str(n)
        else:
            # If not an AP, assume it's a GP (Geometric Progression).
            n = arr[2] ** 2 / arr[1]
            return "GP sequence, " + 'Next number of the sequence:  ' + str(n)

# Test the 'ap_gp_sequence' function with different sequences and print the results.
print(ap_gp_sequence([1, 2, 3]))
print(ap_gp_sequence([2, 6, 18]))
print(ap_gp_sequence([0, 0, 0]))

Sample Output:

AP sequence, Next number of the sequence: 4
GP sequence, Next number of the sequence:  54.0
Wrong Numbers

Explanation:

The above Python code defines a function named "ap_gp_sequence()" that determines whether a given sequence is an Arithmetic Progression (AP) or a Geometric Progression (GP). Here's a brief explanation:

• Function Definition:
• def ap_gp_sequence(arr):: Define a function named "ap_gp_sequence ()" that takes a list of three numbers 'arr' as input.
• Check for Special Case:
• if arr[0] arr[1] arr[2] == 0:: Check if all three elements in the sequence are zero.
• If true, return "Wrong Numbers" since this is not a valid case for an AP or GP.
• Determine AP or GP:
• if arr[1] - arr[0] == arr[2] - arr[1]:: Check if the differences between consecutive elements are equal.
• If true, it's an AP sequence.
• Calculate the next number in the sequence (n) using the AP formula: 2 * arr[2] - arr[1].
• If false, assume it's a GP sequence.
• Calculate the next number in the sequence (n) using the GP formula: arr[2] ** 2 / arr[1].
• Return Result:
• Return a formatted string indicating whether it's an AP or GP sequence and the next number in the sequence.
• Function Testing:
• Test the ap_gp_sequence function with different sequences:
• print(ap_gp_sequence([1, 2, 3])): Test with an AP sequence.
• print(ap_gp_sequence([2, 6, 18])): Test with a GP sequence.
• print(ap_gp_sequence([0, 0, 0])): Test with a special case where all elements are zero.

Visual Presentation:

Flowchart:

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

Previous: Write a Python program to compute the summation of the absolute difference of all distinct pairs in an given array (non-decreasing order).
Next: Write a Python program to print the length of the series and the series from the given 3rd term , 3rd last term and the sum of a series.