Python Challenges: Find the sum of all the positive integers which cannot be written as the sum of two abundant numbers
Write a Python program to find the sum of all the positive integers which cannot be written as the sum of two abundant numbers.
From Wikipedia - Amicable numbers are two different numbers so related that the sum of the proper divisors of each is equal to the other number. (A proper divisor of a number is a positive factor of that number other than the number itself. For example, the proper divisors of 6 are 1, 2, and 3.)
The smallest pair of amicable numbers is (220, 284). They are amicable because the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110, of which the sum is 284; and the proper divisors of 284 are 1, 2, 4, 71 and 142, of which the sum is 220.
Sample Solution:
Python Code:
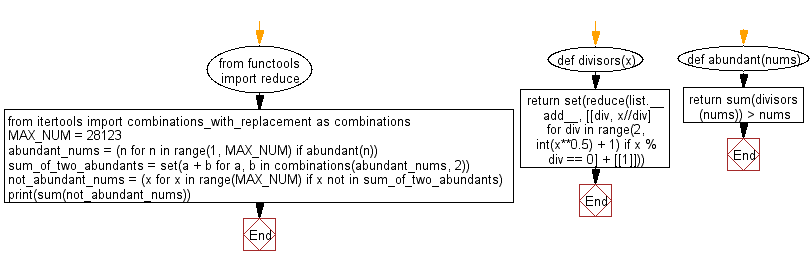
from functools import reduce
from itertools import combinations_with_replacement as combinations
MAX_NUM = 28123
def divisors(x):
return set(reduce(list.__add__, [[div, x//div] for div in range(2, int(x**0.5) + 1) if x % div == 0] + [[1]]))
def abundant(nums):
return sum(divisors(nums)) > nums
abundant_nums = (n for n in range(1, MAX_NUM) if abundant(n))
sum_of_two_abundants = set(a + b for a, b in combinations(abundant_nums, 2))
not_abundant_nums = (x for x in range(MAX_NUM) if x not in sum_of_two_abundants)
print(sum(not_abundant_nums))
Sample Output:
4179871
Flowchart:
Python Code Editor:
Contribute your code and comments through Disqus.
Previous: Write a Python program to compute the sum of all the amicable numbers under a given number.
Next: Write a Python program to find the millionth lexicographic permutation of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
