Python: Compute the median of all elements

Last update on December 21 2024 07:30:29 (UTC/GMT +8 hours)

Write a Python program that adds integer numbers from the data stream to a heapq and computes the median of all elements. Use the heap queue algorithm.

From Wikipedia "In statistics and probability theory, the median is the value separating the higher half from the lower half of a data sample, a population or a probability distribution. For a data set, it may be thought of as the "middle" value. For example, in the data set [1, 3, 3, 6, 7, 8, 9], the median is 6, the fourth largest, and also the fourth smallest, number in the sample. For a continuous probability distribution, the median is the value such that a number is equally likely to fall above or below it."

Sample Solution:

Python Code:

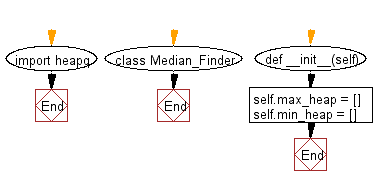
import heapq
class Median_Finder:
    
    def __init__(self):
        #initialize data structure
        self.max_heap = []
        self.min_heap = []
        

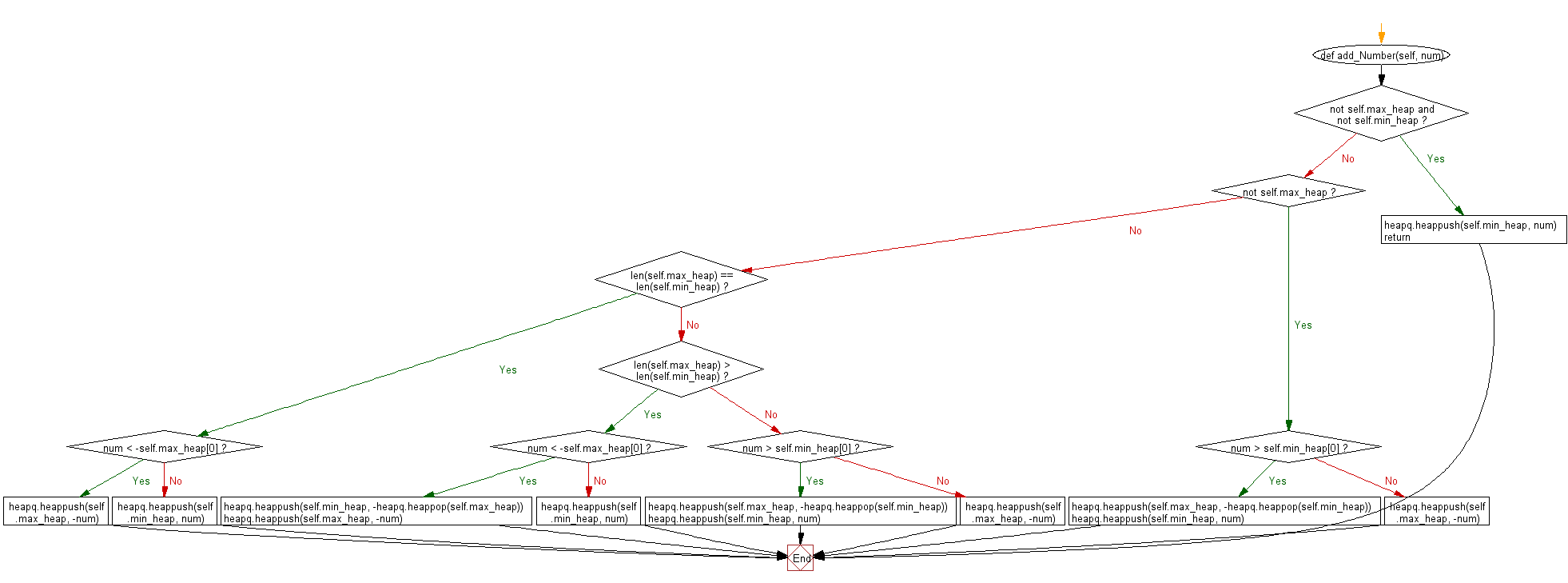
    def add_Number(self, num):
        #type num: int, rtype: void
        if not self.max_heap and not self.min_heap:
            heapq.heappush(self.min_heap, num)
            return 
        if not self.max_heap:
            if num > self.min_heap[0]:
                heapq.heappush(self.max_heap, -heapq.heappop(self.min_heap))
                heapq.heappush(self.min_heap, num)
            else:
                heapq.heappush(self.max_heap, -num)
            return
        if len(self.max_heap) == len(self.min_heap):
            if num < -self.max_heap[0]:
                heapq.heappush(self.max_heap, -num)
            else:
                heapq.heappush(self.min_heap, num)
        elif len(self.max_heap) > len(self.min_heap):
            if num < -self.max_heap[0]:
                heapq.heappush(self.min_heap, -heapq.heappop(self.max_heap))
                heapq.heappush(self.max_heap, -num)
            else:
                heapq.heappush(self.min_heap, num)
        else:
            if num > self.min_heap[0]:
                heapq.heappush(self.max_heap, -heapq.heappop(self.min_heap))
                heapq.heappush(self.min_heap, num)
            else:
                heapq.heappush(self.max_heap, -num)
        

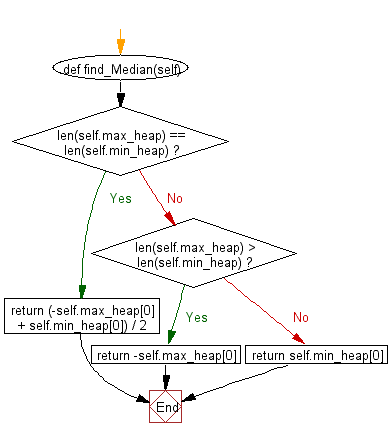
    def find_Median(self):
        #rtype: float
        if len(self.max_heap) == len(self.min_heap):
            return (-self.max_heap[0] + self.min_heap[0]) / 2
        elif len(self.max_heap) > len(self.min_heap):
            return -self.max_heap[0]
        else:
            return self.min_heap[0] 
S = Median_Finder()
S.add_Number(1)
S.add_Number(2)
result = S.find_Median()
print(result)
S.add_Number(3)
result = S.find_Median()
print(result)
S.add_Number(4)
S.add_Number(5)
result = S.find_Median()
print(result)

Sample Output:

1.5
2
3

Flowchart:

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

Previous: Write a Python program to check if the letters of a given string can be rearranged so that two characters that are adjacent to each other are different using Heap queue algorithm.
Next: You are given two integer arrays sorted in ascending order and an integer k. Write a Python program to find k number of pairs (u, v) which consists of one element from the first array and one element from the second array using Heap queue algorithm.