Python List Advanced Exercise - Permutations of the members of a list

Python List Advanced: Exercise-3 with Solution

Write a Python function that finds all the permutations of the members of a list.

In mathematics, the notion of permutation relates to the act of arranging all the members of a set into some sequence or order, or if the set is already ordered, rearranging (reordering) its elements, a process called permuting. These differ from combinations, which are selections of some members of a set where order is disregarded

Sample Solution:

Python Code:

# Define a function to generate all permutations of a list of numbers
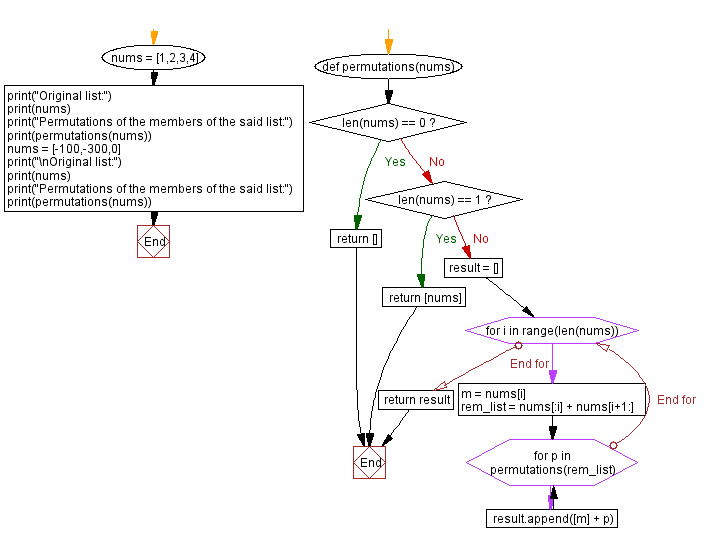
def permutations(nums):
    # Base case: If the input list is empty, return an empty list as there are no permutations.
    if len(nums) == 0:
        return []
    # Base case: If the input list has only one element, return a list containing that element as the only permutation.
    if len(nums) == 1:
        return [nums]
    # Initialize an empty list 'result' to store permutations.
    result = []
    # Iterate over the elements of the input list.
    for i in range(len(nums)):
        # Select an element 'm' at index 'i'.
        m = nums[i]
        # Create a new list 'rem_list' that contains all elements except 'm'.
        rem_list = nums[:i] + nums[i+1:]
        # Recursively find permutations of 'rem_list'.
        for p in permutations(rem_list):
            # Add 'm' to the beginning of each permutation in 'p' and append it to the 'result' list.
            result.append([m] + p)
    # Return the list of all permutations.
    return result

# Create a list of numbers
nums = [1, 2, 3, 4]

# Print the original list
print("Original list:")
print(nums)

# Call the permutations function and print the result, which is a list of all permutations of 'nums'.
print("Permutations of the members of the said list:")
print(permutations(nums))

# Create another list of numbers
nums = [-100, -300, 0]

# Print the original list
print("\nOriginal list:")
print(nums)

# Call the permutations function with the second list and print the result, which is a list of all permutations of 'nums'.
print("Permutations of the members of the said list:")
print(permutations(nums)) 

Sample Output:

Original list:
[1, 2, 3, 4]
Permutations of the members of the said list:
[[1, 2, 3, 4], [1, 2, 4, 3], [1, 3, 2, 4], [1, 3, 4, 2], [1, 4, 2, 3], [1, 4, 3, 2], [2, 1, 3, 4], [2, 1, 4, 3], [2, 3, 1, 4], [2, 3, 4, 1], [2, 4, 1, 3], [2, 4, 3, 1], [3, 1, 2, 4], [3, 1, 4, 2], [3, 2, 1, 4], [3, 2, 4, 1], [3, 4, 1, 2], [3, 4, 2, 1], [4, 1, 2, 3], [4, 1, 3, 2], [4, 2, 1, 3], [4, 2, 3, 1], [4, 3, 1, 2], [4, 3, 2, 1]]

Original list:
[-100, -300, 0]
Permutations of the members of the said list:
[[-100, -300, 0], [-100, 0, -300], [-300, -100, 0], [-300, 0, -100], [0, -100, -300], [0, -300, -100]]

Flowchart:

What is the time complexity and space complexity of the following Python code?

def permutations(nums):
    if len(nums) == 0:
        return []
    if len(nums) == 1:
        return [nums]
    result = []
    for i in range(len(nums)):
        m = nums[i]
        rem_list = nums[:i] + nums[i+1:]
        for p in permutations(rem_list):
            result.append([m] + p)
    return result

Time complexity - The time complexity of the said code is O(n!), where n is the length of the input array “nums”. This is because the code generates all possible permutations of the input array, and there are n! possible permutations.

Space complexity - As the code generates a list of n! permutations, each of which contains n elements, the space complexity of the code is also O(n!). Therefore, the total amount of space used by the code is O(n *n!), which simplifies to O(n!).

Python Code Editor:

Previous: Length of the longest increasing sub-sequence.
Next: Find the k^th smallest element in a list.