Python Math: Describe linear regression

Last update on December 21 2024 07:34:54 (UTC/GMT +8 hours)

Write a Python program to describe linear regression .

Note : A linear regression line has an equation of the form Y = a + bX, where X is the explanatory variable and Y is the dependent variable. The slope of the line is b, and a is the intercept (the value of y when x = 0).

Sample Solution:

Python Code:

#https://gist.github.com/cartr/6513044
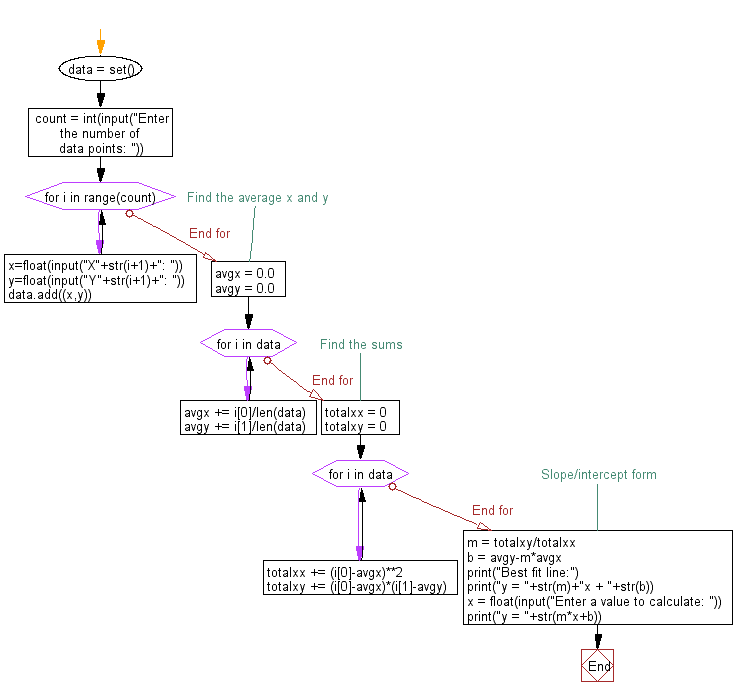
# Define the data
data = set()
count = int(input("Enter the number of data points: "))
for i in range(count):
    x=float(input("X"+str(i+1)+": "))
    y=float(input("Y"+str(i+1)+": "))
    data.add((x,y))

# Find the average x and y
avgx = 0.0
avgy = 0.0
for i in data:
    avgx += i[0]/len(data)
    avgy += i[1]/len(data)

# Find the sums
totalxx = 0
totalxy = 0

for i in data:
    totalxx += (i[0]-avgx)**2
    totalxy += (i[0]-avgx)*(i[1]-avgy)

# Slope/intercept form
m = totalxy/totalxx
b = avgy-m*avgx

print("Best fit line:")
print("y = "+str(m)+"x + "+str(b))

x = float(input("Enter a value to calculate: "))
print("y = "+str(m*x+b))

Sample Output:

Enter the number of data points: 2                                                                            
X1: 1                                                                                                         
Y1: 2                                                                                                         
X2: 3                                                                                                         
Y2: 4                                                                                                         
Best fit line:                                                                                                
y = 1.0x + 1.0                                                                                                
Enter a value to calculate: 10                                                                                
y = 11.0

Flowchart:

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

Previous: Write a Python program to parse math formulas and put parentheses around multiplication and division.
Next: Write a Python program to calculate a grid of hexagon coordinates of the given radius given lower-left and upper-right coordinates. The function will return a list of lists containing 6 tuples of x, y point coordinates. These can be used to construct valid regular hexagonal polygons.