Python Math: Implement Euclidean Algorithm to compute the greatest common divisor

Last update on December 21 2024 07:35:02 (UTC/GMT +8 hours)

Write a Python program to implement the Euclidean Algorithm to compute the greatest common divisor (GCD).

Note: In mathematics, the Euclidean algorithm[a], or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two numbers, the largest number that divides both of them without leaving a remainder.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 147 = 252 − 105.

Sample Solution:

Python Code:

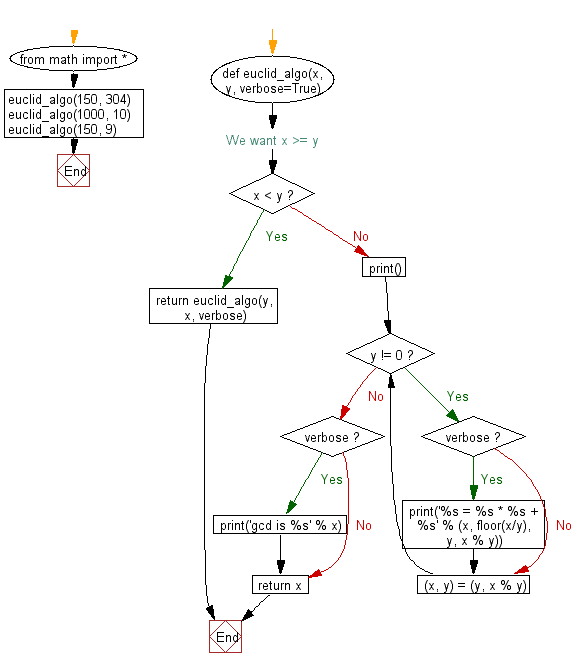
from math import *

def euclid_algo(x, y, verbose=True):
	if x < y: # We want x >= y
		return euclid_algo(y, x, verbose)
	print()
	while y != 0:
		if verbose: print('%s = %s * %s + %s' % (x, floor(x/y), y, x % y))
		(x, y) = (y, x % y)
	
	if verbose: print('gcd is %s' % x) 
	return x


euclid_algo(150, 304)
euclid_algo(1000, 10)
euclid_algo(150, 9)

Sample Output:

304 = 2 * 150 + 4                                                                                             
150 = 37 * 4 + 2                                                                                              
4 = 2 * 2 + 0                                                                                                 
gcd is 2                                                                                                      
                                                                                                              
1000 = 100 * 10 + 0                                                                                           
gcd is 10                                                                                                     
                                                                                                              
150 = 16 * 9 + 6                                                                                              
9 = 1 * 6 + 3                                                                                                 
6 = 2 * 3 + 0                                                                                                 
gcd is 3

Pictorial Presentation:

Flowchart:

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

Previous: Write a Python program to calculate clusters using Hierarchical Clustering method.
Next: Write a Python program to convert RGB color to HSV color.