Fit a statistical model using MLE with NumPy and SciPy

Last update on December 21 2024 07:36:53 (UTC/GMT +8 hours)

NumPy: Integration with SciPy Exercise-19 with Solution

Write a NumPy program to generate a set of data and fit a statistical model using SciPy's optimize module for maximum likelihood estimation (MLE).

Sample Solution:

Python Code:

import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt

# Generate synthetic data: sample from a normal distribution
np.random.seed(42)
data = np.random.normal(loc=5.0, scale=2.0, size=1000)

# Define the negative log-likelihood function for a normal distribution
def neg_log_likelihood(params):
    mu, sigma = params
    if sigma <= 0:
        return np.inf
    nll = -np.sum(np.log(1/(np.sqrt(2 * np.pi) * sigma) * np.exp(-(data - mu)**2 / (2 * sigma**2))))
    return nll

# Initial guess for the parameters (mean and standard deviation)
initial_params = np.array([0.0, 1.0])

# Perform MLE using SciPy's minimize function
result = minimize(neg_log_likelihood, initial_params, method='L-BFGS-B', bounds=[(None, None), (1e-5, None)])

# Extract the estimated parameters
mu_mle, sigma_mle = result.x

# Print the results
print(f"Estimated mean (mu): {mu_mle:.3f}")
print(f"Estimated standard deviation (sigma): {sigma_mle:.3f}")

# Plot the data and the fitted normal distribution
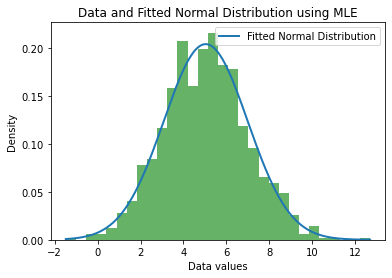
plt.hist(data, bins=30, density=True, alpha=0.6, color='g')

# Plot the fitted normal distribution
x = np.linspace(min(data), max(data), 1000)
fitted_pdf = (1/(np.sqrt(2 * np.pi) * sigma_mle)) * np.exp(-(x - mu_mle)**2 / (2 * sigma_mle**2))
plt.plot(x, fitted_pdf, label='Fitted Normal Distribution', linewidth=2)

plt.xlabel('Data values')
plt.ylabel('Density')
plt.title('Data and Fitted Normal Distribution using MLE')
plt.legend()
plt.show()

Output:

Explanation:

• Import libraries:
• Import the necessary modules from NumPy, SciPy, and Matplotlib.
• Generate synthetic data:
• Create a sample dataset from a normal distribution using NumPy.
• Define the negative log-likelihood function:
• Define the function for the negative log-likelihood of a normal distribution.
• Initial guess:
• Provide an initial guess for the parameters (mean and standard deviation).
• Perform MLE:
• Use SciPy's minimize function with the L-BFGS-B method to find the parameters that minimize the negative log-likelihood.
• Extract parameters:
• Retrieve the estimated parameters (mean and standard deviation) from the result.
• Print results:
• Output the estimated parameters.
• Use Matplotlib to visualize the histogram of the data and the fitted normal distribution.

Python-Numpy Code Editor: