NumPy: Compute the cross product of two given vectors

Last update on May 05 2025 10:44:20 (UTC/GMT +8 hours)

3. Cross Product of Vectors

Write a NumPy program to compute the cross product of two given vectors.

NumPy: Cross product of two vectors

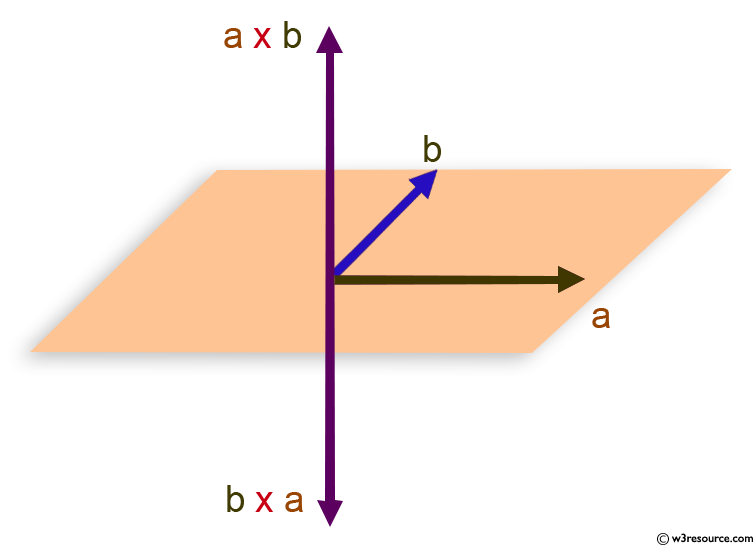
NumPy Linear algebra: Compute the cross product of two given vectors

Sample Solution :

Python Code :

import numpy as np

# Define two 2x2 matrices 'p' and 'q'
p = [[1, 0], [0, 1]]
q = [[1, 2], [3, 4]]

# Display the original matrices 'p' and 'q'
print("Original matrices:")
print(p)
print(q)

# Compute the cross product of matrices 'p' and 'q' using np.cross for both orders p x q and q x p
result1 = np.cross(p, q)
result2 = np.cross(q, p)

# Display the cross product of the matrices for both orders
print("Cross product of the said two vectors (p, q):")
print(result1)
print("Cross product of the said two vectors (q, p):")
print(result2)

Sample Output:

original matrix:
[[1, 0], [0, 1]]
[[1, 2], [3, 4]]
cross product of the said two vectors(p, q):
[ 2 -3]
cross product of the said two vectors(q, p):
[-2  3]

Explanation:

p = [[1, 0], [0, 1]]

q = [[1, 2], [3, 4]]

At first two 2x2 matrixes p and q have been declared.

result1 = np.cross(p, q) calculates the cross product of p and q.

p = [[1, 0, 0],

[0, 1, 0]]

q = [[1, 2, 0],

[3, 4, 0]]

Now, calculate the cross product:

result1[0] = p[0] x q[0] = (0, 0, 2)

result1[1] = p[1] x q[1] = (0, 0, -2)

Thus, result1 is a 2x3 matrix:

[[ 0, 0, 2],

[ 0, 0, -2]]

result2 = np.cross(q, p) calculates the cross product of q and p (reversing the order of operands):

result2[0] = q[0] x p[0] = (0, 0, -2)

result2[1] = q[1] x p[1] = (0, 0, 2)

Thus, result2 is a 2x3 matrix:

[[ 0, 0, -2],

[ 0, 0, 2]]

For more Practice: Solve these Related Problems:

Compute the cross product of two 3D vectors using np.cross and verify that the result is orthogonal to both inputs.
Implement a function that computes the cross product for an array of vectors (batch processing) using vectorized operations.
Validate the cross product by comparing its magnitude to the area of the parallelogram defined by the vectors.
Manually compute the cross product using a determinant-based approach and compare it with np.cross output.

Go to:

PREV : Outer Product of Vectors
NEXT : Determinant of a Square Array

Python-Numpy Code Editor:

What is the difficulty level of this exercise?

Test your Programming skills with w3resource's quiz.