NumPy: Compute the determinant of a given square array

NumPy: Linear Algebra Exercise-4 with Solution

Write a NumPy program to compute the determinant of a given square array.

From Wikipedia: In linear algebra, the determinant is a value that can be computed from the elements of a square matrix. The determinant of a matrix A is denoted det(A), det A, or |A|. Geometrically, it can be viewed as the scaling factor of the linear transformation described by the matrix.

In the case of a 2 × 2 matrix the determinant may be defined as:

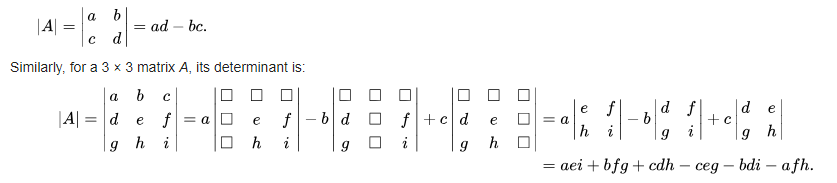
Sample Solution:

Python Code :

import numpy as np
from numpy import linalg as LA

# Create a 2x2 array 'a'
a = np.array([[1, 0], [1, 2]])

# Display the original 2x2 array 'a'
print("Original 2-d array")
print(a)

# Compute the determinant of the 2-D array 'a' using np.linalg.det()
print("Determinant of the said 2-D array:")
print(np.linalg.det(a)) 

Sample Output:

Original 2-d array
[[1 0]
 [1 2]]
Determinant of the said 2-D array:
2.0

Explanation:

The above NumPy code calculates the determinant of a 2x2 matrix.

from numpy import linalg as LA: This line imports the linalg module from NumPy and aliases it as LA. The linalg module contains various linear algebra functions, such as calculating determinants, solving linear equations, etc.

a = np.array([[1, 0], [1, 2]]): This line creates a 2x2 matrix a represented as a NumPy array:

print(np.linalg.det(a)): This line calculates the determinant of the matrix a using the det function from the linalg module (imported as LA). The determinant of a 2x2 matrix [[a, b], [c, d]] is calculated as (a * d) - (b * c). In this case, the determinant of matrix a is (1 * 2) - (0 * 1) = 2. Finally print() function prints the result to the console.

Python-Numpy Code Editor:

Previous: Write a NumPy program to compute the cross product of two given vectors.
Next: Write a NumPy program to evaluate Einstein’s summation convention of two given multidimensional arrays.