NumPy: Compute the Kronecker product of two given mulitdimension arrays

Last update on December 21 2024 07:51:44 (UTC/GMT +8 hours)

Write a NumPy program to compute the Kronecker product of two given mulitdimension arrays.

Note: In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It is a generalization of the outer product (which is denoted by the same symbol) from vectors to matrices, and gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix multiplication, which is an entirely different operation.

If A is an m × n matrix and B is a p × q matrix, then the Kronecker product A ⊗ B is the mp × nq block matrix:

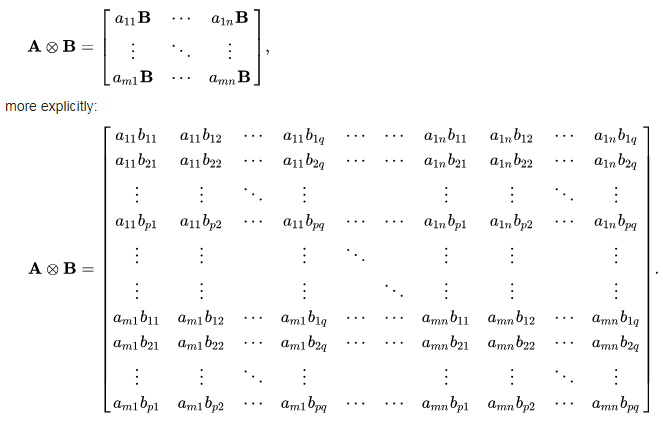
Sample Solution :

Python Code :

import numpy as np

# Create two 1-dimensional arrays 'a' and 'b'
a = np.array([1, 2, 3])
b = np.array([0, 1, 0])

# Display the original 1-d arrays 'a' and 'b'
print("Original 1-d arrays:")
print(a)
print(b)

# Compute the Kronecker product of the arrays 'a' and 'b' using np.kron() function
result = np.kron(a, b)

# Display the Kronecker product of the said arrays
print("Kronecker product of the said arrays:")
print(result)

# Create two 3x3 arrays 'x' and 'y'
x = np.arange(9).reshape(3, 3)
y = np.arange(3, 12).reshape(3, 3)

# Display the original higher dimension arrays 'x' and 'y'
print("Original Higher dimension:")
print(x)
print(y)

# Compute the Kronecker product of the arrays 'x' and 'y' using np.kron() function
result = np.kron(x, y)

# Display the Kronecker product of the said arrays
print("Kronecker product of the said arrays:")
print(result) 

Sample Output:

Original 1-d arrays:
[1 2 3]
[0 1 0]
Kronecker product of the said arrays:
[0 1 0 0 2 0 0 3 0]
Original Higher dimension:
[[0 1 2]
 [3 4 5]
 [6 7 8]]
[[ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]]
Kronecker product  of the said arrays:
[[ 0  0  0  3  4  5  6  8 10]
 [ 0  0  0  6  7  8 12 14 16]
 [ 0  0  0  9 10 11 18 20 22]
 [ 9 12 15 12 16 20 15 20 25]
 [18 21 24 24 28 32 30 35 40]
 [27 30 33 36 40 44 45 50 55]
 [18 24 30 21 28 35 24 32 40]
 [36 42 48 42 49 56 48 56 64]
 [54 60 66 63 70 77 72 80 88]]

Explanation:

In the above exercise –

a = np.array([1, 2, 3]): This line creates a 1D NumPy array a with elements [1, 2, 3].

b = np.array([0, 1, 0]): This line creates a 1D NumPy array b with elements [0, 1, 0].

result = np.kron(a, b): This line computes the Kronecker product of the two arrays a and b. The Kronecker product is obtained by multiplying each element of the first array with the entire second array. In this case, the result is [0, 1, 0, 0, 2, 0, 0, 3, 0].

x = np.arange(9).reshape(3, 3): This line creates a 3x3 NumPy array x containing elements from 0 to 8, arranged in a 3x3 matrix:

[[0, 1, 2],

[3, 4, 5],

[6, 7, 8]]

y = np.arange(3, 12).reshape(3, 3): This line creates a 3x3 NumPy array y containing elements from 3 to 11, arranged in a 3x3 matrix:

[[ 3, 4, 5],

[ 6, 7, 8],

[ 9, 10, 11]]

result = np.kron(x, y): This line computes the Kronecker product of the two arrays x and y. The result is a 9x9 array formed by multiplying each element of x with the entire y array.

print(result): This line prints the resulting Kronecker product, which is a 9x9 array.

Python-Numpy Code Editor: