Ordinary differential equations with NumPy and SciPy

Last update on December 21 2024 07:37:17 (UTC/GMT +8 hours)

NumPy: Integration with SciPy Exercise-8 with Solution

Write a Numpy program to create a NumPy array and use SciPy to solve a system of ordinary differential equations (ODEs).

Sample Solution:

Python Code:

# Import necessary libraries
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# Define the system of ODEs
def model(y, t):
    dydt = -2 * y + np.sin(t)
    return dydt

# Create a NumPy array for initial conditions
y0 = np.array([1.0])

# Create a time array using NumPy
t = np.linspace(0, 10, 100)

# Use SciPy's odeint function to solve the ODEs
solution = odeint(model, y0, t)

# Plot the solution
plt.plot(t, solution)
plt.xlabel('Time')
plt.ylabel('y(t)')
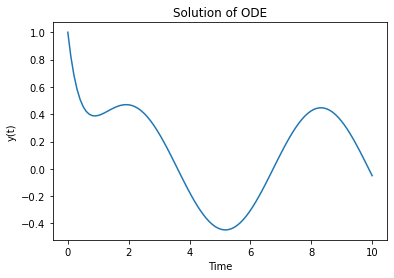
plt.title('Solution of ODE')
plt.show()

Output:

Explanation:

• Import necessary libraries:
• Import NumPy for array operations, SciPy's odeint function for solving ODEs, and Matplotlib for plotting.
• Define the system of ODEs:
• Create a function model that represents the ODE dydt=−2y+sin⁡(t)\frac{dy}{dt} = -2y + \sin(t)dtdy=−2y+sin(t).
• Create a NumPy array for initial conditions:
• Initialize the starting value of yyy.
• Create a time array using NumPy:
• Generate an array of time points from 0 to 10.
• Use SciPy's odeint function to solve the ODEs:
• Pass the model, initial condition, and time array to odeint to solve the ODE.
• Finally use Matplotlib to visualize the solution of the ODE over time.

Python-Numpy Code Editor: